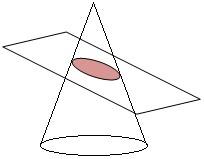
By intersecting a cone with a plane, a curve is obtained and is named conic section, which is the red area shown above.
The expression for a conic section in the Cartesian coordinate system is defined as:
Ax2 + Bxy + Cy2 + Dx + Ey + F = 0
A ≠ 0, B ≠ 0 and C ≠ 0
The result of B2 – 4AC determines the type of the conic section obtained:
• If the result is smaller than 0, then we have an ellipse, unless the conic is degenerate.
o The ellipse is defined as: x2/a2 + y2/b2 = 1 and x2/b2 + y2/a2 = 1
• If the result is smaller than 0 and A=C, B=0 then we have a perfect circle.
o The circle is defined as: x2 + y2 = r2
• If the result is equal to 0, then we have a parabola.
o The parabola is defined as: y2 = 4 ∙ a ∙ x and x2 = 4 ∙ a ∙ y
• If the result is bigger than 0, then we have a hyperbola.
o The hyperbola is defined as: x2/a2 – y2/b2 = 1 and y2/a2 – x2/b2 = 1
• If the result is bigger than 0 and A+C = 0, then we have a rectangular hyperbola.
o The rectangular hyperbola is defined as: x ∙ y = c2
Example
If the hyperbola passes through the focus of the ellipse x2/25 + y2/16 = 1 and its transverse and conjugate axes coincide with the major and minor axes of the ellipse, and the product of the eccentricities is 1, then:
The equation of the hyperbola is x2/9 – y2/16 = 1 and foci is (5,0)
The equation of the hyperbola is x2/9 – y2/25 = 1 and foci is (5,0)
The equation of the hyperbola is x2/25 – y2/16 = 1 and foci is (5,0)
Focus of the hyperbola is (3,0)
NOTE:
An ellipse with centre at the origin (0,0) is the graph of:
x2/a2 + y2/b2= 1
or
x2/b2 + y2/a2 = 1,
where a > b > 0.
The length of the major axis is 2a, and the length of the minor axis is 2b. The two foci (foci is the plural of focus) are at (± c, 0) or at (0, ± c), where c2 = a2 - b2.
The eccentricy of an ellipse is a measure of how nearly circular the ellipse. Eccentricity is found by the following formula:
Eccentricity = c/a,
where c is the distance from the centre to the focus of the ellipse and a is the distance from the centre to a vertex.
The eccentricity of the hyperbola e is given by the relation e = sqrt (1 + b2/a2)
Summary of Basic Properties
|
|
Circle
|
Ellipse
|
Parabola
|
Hyperbola
|
|
Standard Cartesian Equation :
|
x2 + y2 = r2
|
x2/a2 + y2/b2= 1
|
y2 = 4ax
|
x2/a2 - y2/b2= 1
|
|
Eccentricity (e):
|
0
|
0 < e <1
|
1
|
1 < e
|
|
Relation between a,b and e
|
b = a
|
b2 = a2(1-e2)
|
|
b2 = a2(e2-1)
|
|
Parametric Representation
|
|
x = a · cosθ
y = b · sinθ
|
x = at2
y = 2at
|
x = a · secθ
y = b · tanθ
or
x = ½ * a(t + 1/t)
y = ½ * b(t - 1/t)
|
|
Definition: It is the locus of all points which meet the condition...
|
distance to the origin is constant
|
sum of distances to each focus is constant
|
distance to focus = distance to directrix
|
difference between distances to each foci is constant
|
It might tidy the logic up to consider a circle to be a special case of an ellipse. Then there are two 'main' classes
an ellipse, with e < 1
a hyperbola, with e > 1
and a 'critical' class - the parabola with e = 1.
The General Equation for a Conic is
Ax2 + Bxy + Cy2 + Dx + Ey + F = 0
A ≠ 0, B ≠ 0 and C ≠ 0
The actual type of conic can be found from the sign of B2 - 4AC
|
B2 - 4AC
|
Then the curve is
|
|
< 0
|
Ellipse, circle, point or no curve.
|
|
= 0
|
Parabola, 2 parallel lines, 1 line or no curve.
|
|
> 0
|
Hyperbola or 2 intersecting lines.
|
Note: the above notation brings a close analogy with the formulas of quadratic equations. Sometimes, however, the formula is stated slightly differently
Ax2 + 2Bxy + Cy2 + Dx + Ey + F = 0
Here the type of conic must be found from the sign of B2 - AC
|
B2 - AC
|
Then the curve is
|
|
< 0
|
Ellipse, circle, point or no curve.
|
|
= 0
|
Parabola, 2 parallel lines, 1 line or no curve.
|
|
> 0
|
Hyperbola or 2 intersecting lines.
|
Polar Form
For an origin at a focus, the general polar form (apart from a circle) is
1 + e · cosθ = L / r
where L is the semi latus rectum.
Ellipse
The Cartesian equation of an ellipse is
x2/a2 + y2/b2= 1
where a and b would give the lengths of the semi-major and semi-minor axes. In its general form, with the origin at the centre of coordinates we have:
|
the foci are at (±ae, 0), where e is the eccentricity of the ellipse
|
|
the directrix are at x = ±a/e, where e is the eccentricity of the ellipse
|
|
the major axis of length: 2a
|
|
the minor axis is of length: 2b
|
|
the semi latus rectum is of length: 2b2 / a
|
Example
Find the foci and the equation of the hyperbola with the vertices (0,±1) and asymptote y = 2x
Recall the formulas for hyperbola mentioned in the beginning:
For hyperbola x2/a2 – y2/b2 = 1 it has:
foci (±c, 0), where c2 = a2 + b2
vertices (±a, 0)
and asymptotes y = ±(b/a)x.
For hyperbola y2/a2 – x2/b2 = 1 it has:
foci (0, ±c), where c2 = a2 + b2
vertices (0, ±a),
and asymptotes y = ±(a/b)x
In this example we will use the second formula namely y2/a2 – x2/b2 = 1 to determine its equation.
We can see that a=1 and a/b = 2 according to the values given in the example. Thus b=a/2 = 1/2 and c2 = a2 + b2 = 5/4 and the foci are (0, ±√5/2). Inserting these values will give us the final equation of the hyperbola, namely y2 - 4x2 = 1.
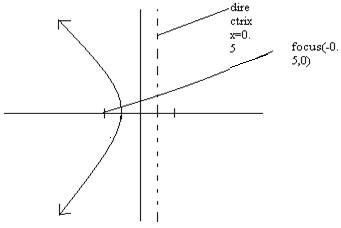
Example
Find the focus and directrix for y2 = -2x.
From the given equation of the parabola, we have x = - y2/2, which is obtained by isolating x from the equation. The minus sign flips the parabola to the left, so we have: 1/4p = -1/2 → p = -1/2. Therefore, focus and directrix are (-1/2, 0) and x = 1/2.
Below is a sketch of the parabola.