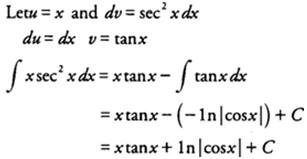The 6 basic hyperbolic functions are defined by:
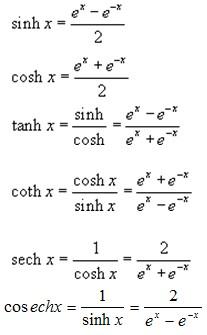
Example 1: Evaluate the integral ∫sech2(x)dx
Solution:
We know that the derivative of tanh(x) is sech2(x), so the integral of sech2(x) is just:
tanh(x)+c.
Example 2: Calculate the integral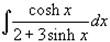 
.
Solution : We make the substitution: u = 2 + 3sinh x, du = 3cosh x dx. Then cosh x dx = du/3.
Hence, the integral is
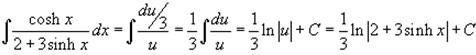
Example 3: Calculate the integral ∫sinh2x cosh3x dx
Solution:
Applying the formulas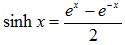 
and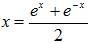 
, we get:
Example 4: Evaluate ∫ x sech2 x dx.
Solution:
