
The area of any polygon is given by:
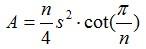
or
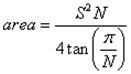
where,
S is the length of any side
N is the number of sides
π is PI, approximately 3.142
NOTE: The area of a polygon that has infinite sides is the same as the area a circle.
Depending on the information that are given, different formulas can be used to determine the area of a polygon, below is a list of these formulas:
The length of a side is given:
By definition, all sides of a regular polygon are equal in length. If you know the length of one of the sides, the area is given by the formula:
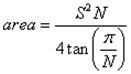
Given the radius (circumradius)
If you know the radius (distance from the center to a vertex)
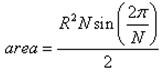
where
R is the radius (circumradius)
N is the number of sides
π is PI, approximately 3.142
sin is the sine function calculated in radians
Given the apothem (inradius)
If you know the apothem, or inradius, (the perpendicular distance from center to a side).
area = A2Ntan(π/N)
where,
A is the length of the apothem (inradius)
N is the number of sides
tan is the tangent function calculated in radians
Given the apothem and length of a side
If you know the apothem (the perpendicular distance from center to a side) and the length of a side, first determine the perimeter by mutiplying the side length by N. The area is given by:
area = AP/2
where
A is the length of the apothem
P is the perimeter
Example 1: Find the area of a polygon with the given radius 2 m and the number of sides is 5 using Apothem.
Solution:
Step 1: Find the apothem.
Apothem = R * cos(π/N)
Apothem = 2 * cos(3.14 / 5)
Apothem = 2 * cos(0.63)
Apothem = 2 * 0.81
Apothem = 1.62 m
Step 2: Find the area.
Area = A² * N * tan(π/N)
Area = 1.62² * 5 * tan(3.14 / 5)
Area = 2.62 * 5 * tan(0.63)
Area = 13.1 * 0.73
Area = 9.5 m2
Example 2: The heptagon side length is 7.0 cm calculate the area of the heptagon?
Solution:
Area = S2N / (4tan(π/N ))
The side length S is 7.0 cm and N is the 7 because heptagon has 7 sides, the area can be determined by using the formula below:
Area = 343 / (4tan(π/N ))
Area = 343 / (4tan(3.14/7))
Area = 178.18 cm2
Example 3: Calculate the area of a regular polygon with 9 sides and an inradius of 7 cm.
Solution:
Area = A² * N * tan(π/N), where A is the inradius
Area =72×9 × tan(π/9)
Area = 49 × 9 × 0.3639 = 160.4799 cm2
Example 4: Calculate the area of the polygon with a circumradius of 4 cm and 9 sides.
Solution: Area using the circumradius formula:
Area = R2×N×sin(2π/N) / 2
Area = 42×9×sin(2π/9) / 2
Area =16×9×0.643/2 = 92.59cm2
Example 5: If the side of a regular hexagon is equal to 4 cm and apothem is equal to the measure of 5 cm. Calculate the measure of the area of a regular hexagon.
Solution:
The given regular polygon is hexagon and we know that hexagon has 6 equal sides; each side’s is 4 cm in length; apothem is equal to 5 cm.
The area of the polygon is calculated using the following formula:
Area = AP/2, where A is apothem and P is the perimeter of the polygon
The perimeter of the polygon is easily determined by multiply the length of each side with the number of sides, which gives:
P = 4 * 6 = 24 cm
Now we have to substitute the perimeter and apothem values in the above formula, then we have:
Area = AP/2
Area = 5 × 24 / 2 = 60 cm2
Online Area Calculator