Solving logarithmic functions using Logarithmic Identities
Example 1: Solve log2(x) + log2(x – 2) = 3
Solution: Here we need to use logarithmic identities to combine the two terms on the left-hand side of the equation:
log2(x) + log2(x – 2) = 3
log2 ((x) (x – 2)) = 3
log2(x2 – 2x) = 3
Then we’ll use the relationship to convert the log form to the corresponding exponential form, and then move further,
log2(x2 – 2x) = 3
23 = x2 – 2x
8 = x2 – 2x
0 = x2 – 2x – 8
0 = (x – 4) (x + 2)
x = 4, –2
But if x = –2, then "log2(x)", from the original logarithmic equation, will have a negative number for its argument (as will the term "log2(x – 2)"). Since logs cannot have zero or negative arguments, then the solution to the original equation cannot be x = –2.
The solution is x = 4.
Example 2: Solve log2(x2) = (log2(x)) 2.
Solution: First, we'll write out the square on the right-hand side:
log2(x2) = (log2(x)) 2
log2(x2) = (log2(x)) (log2(x))
Then we’ll apply the log rule to move the "squared", from inside the log on the left-hand side of the equation, out in front of that log as a multiplier. Then we'll move that term to the right-hand side:
2log2(x) = [log2(x)] [log2(x)]
0 = [log2(x)] [log2(x)] – 2log2(x)
Factorize the above equation to obtain
0 = [log2(x)] [log2(x) – 2]
log2(x) = 0 or log2(x) – 2 = 0
20 = x or log2(x) = 2
1 = x or 22 = x
1 = x or 4 = x
Example 3: Solve 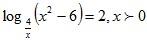
Solution: Since 4/x is the base of a log function x is greater than 0.
The equation is then equivalent with (4/x) 2 = x2- 6
<=> 16 = x4- 6x2
Now, let x2 = t
<=> 16 = t2- 6t
<=> t=-2 or t=8
<=> x = sqrt (8) (since x >0)
The solution is x = 1, 4.